Eulerian & Hamiltonian - MATH-CS COMPASS

Eulerian

The PATH problem asks whether a directed path exists from vertex \(s\) to vertex \(t\). In this section, we explore key path-related concepts that bridge computer science and mathematics.

A graph is called Eulerian if it contains an Eulerian cycle (Euler tour) - a closed walk that traverses every edge exactly once allowing for revisiting vertices. This idea originates from Leonhard Euler's groundbreaking work on the Seven Bridges of Königsberg, which laid the foundations of graph theory.

Theorem 1 (Euler 1736): A connected graph is Eulerian if and only if every vertex has even degree.

Similarly, a graph is called semi-Eulerian if it contains an Eulerian path (Eulerian trail) - any trail that traverses every edge of a graph exactly once, but it does not have to be closed - it may start and end at different vertices.

Graph 1 is Eulerian since every vertex has degree 2.
Graph 2 is Semi-Eulerian since it has a Eulerian path, but not cycle.
Graph 3 is Eulerian since vertex A has degree 4, and the others have degree 2.

In Graph 3, we have to "revisit" the vertex A to construct an Eulerian cycle. On the other hand, Graph 1 does not require revisiting vertices (except for starting vertex which is visited twice as it closes the cycle).

Hamiltonian

A graph is called Hamiltonian if it contains a Hamiltonian cycle, which is a closed path that visits every vertex exactly once except for starting vertex.

So, Graph 1 is Hamiltonian, but Graph 3 is not Hamiltonian. Since the Hamiltonian cycle only care about vertices, we don't have to use all edges in the graph to construct the cyle. So, a graph is Hamiltonian does not imply it is Eulerian. For example, the following Graph 4 is Hamiltonian but not Eulerian.

(For instance, there is a Hamiltonian cycle: \(A \to G \to C \to I \to K \to H \to B \to F \to E \to D \to J \to A\).)

By Theorem 1, determining whether or not a given graph has a Eulerian is not hard( it's in the class P ), but deciding whether it is Hamiltonian is much harder(it's in the class NP-complete) because there is no good characterization is known. Note that even though it is hard to determine whether or not a given graph is Hamiltonian, if someone gives you a proposed Hamiltonian cycle, it is easy to verify it in polynomial time by checking that it visits each vertex exactly once and forms a valid cycle.

Is Hamiltonian Cycle?

Let's make an adjacency matrix for Graph 4: \[ G_4 = \begin{bmatrix} 0 & 1 & 0 & 0 & 1 & 0 & 1 & 0 & 0 & 1 & 0 \\ 1 & 0 & 1 & 0 & 0 & 1 & 0 & 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 1 & 0 & 0 & 1 & 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 & 1 & 0 & 0 & 1 & 0 & 1 & 0 \\ 1 & 0 & 0 & 1 & 0 & 1 & 0 & 0 & 1 & 0 & 0 \\ 0 & 1 & 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 1 \\ 1 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 \\ 0 & 1 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 1 \\ 0 & 0 & 1 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 1 \\ 1 & 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 1 \\ 0 & 0 & 0 & 0 & 0 & 1 & 1 & 1 & 1 & 1 & 0 \end{bmatrix} \] In the adjacency matrix, the \((i, j)\)th entry is 1 if there is an edge from vertex \(i\) to vertex \(j\), and 0 if not. For example, the first row represents connections between vertex A and all vertices including vertex A itself.

Let \(n\) be the number of vertices in a given graph. The adjacency matrix requires \(O(n^2)\) "memory space." So far, we have discussed only time complexity, in other words, the "performance" for certain operations. However, real computer does not have infinite memory size. Space complexity does matter. The adjacency matrix has \(O(n^2)\) space complexity. For large \(n\), it costs too much memory space, and most real-world graphs are sparse (few edges compared to \(n^2\) possible edges), so using the adjacency matrix can be wasteful. In the following code, we use the adjacency list instead of the adjacency matrix.

      
                            # Chek if a given cycle in the graph is Hamiltonian cycle or not : O(n)
                            # Here, we don't run this function. 
                            def is_hamiltonian_cycle(adj_matrix, cycle):
                                n = len(adj_matrix)  # get number of vertices
                                # Check cycle length: must visit all vertices and return to start
                                if len(cycle) != n + 1:
                                    return False
                                # Check starts and ends at the same vertex
                                if cycle[0] != cycle[n]: 
                                    return False
                                # Check all vertices (except last) are unique and cover all vertices
                                visited = set(cycle[:n])
                                if len(visited) != n:
                                    return False
                                # Check edges between consecutive vertices
                                for i in range(n):
                                    s, t = cycle[i], cycle[i + 1]
                                    if adj_matrix[s][t] == 0:  # No edge between u and v
                                        return False
                                return True

                            # Convert adjacency matrix to adjacency List
                            def matrix_to_adj_list(adj_matrix):
                                adj_list = {}
                                n = len(adj_matrix)
                                for i in range(n):
                                    adj_list[i] = set()
                                    for j in range(n):
                                        if adj_matrix[i][j] == 1:
                                            adj_list[i].add(j)
                                return adj_list

                            # for adjacency List (We use this one!)
                            def is_hamiltonian_cycle_list(adj_list, cycle):
                                n = len(adj_list)  # number of vertices
                                
                                if len(cycle) != n + 1:
                                    return False
                                
                                if cycle[0] != cycle[n]:
                                    return False
                                visited = set(cycle[:n])
                                
                                if len(visited) != n:
                                    return False
                                
                                for i in range(n):
                                    s, t = cycle[i], cycle[i + 1]
                                    if t not in adj_list[s]:
                                        return False
                                    
                                return True

                            # Convert the vertex numbers (0, 1, ...,) to letters (A, B, ...,) 
                            def print_adj_list(adj_list):
                                print("Adjacency List: ")
                                for v in adj_list:
                                    v_char = chr(ord('A') + v)
                                    neighbors = [chr(ord('A') + u) for u in adj_list[v]]
                                    neighbors_str = ', '.join(sorted(neighbors))
                                    print(f"{v_char}: {neighbors_str}")
                                print()  
                                    
                            # Print cycle and its result
                            def print_cycle_with_result(cycle, adj_list):
                                cycle_letters = [chr(ord('A') + v) for v in cycle]
                                print("Cycle: ", " → ".join(cycle_letters))
                                is_hamiltonian = is_hamiltonian_cycle_list(adj_list, cycle)
                                print("Is this Hamiltonian?:", is_hamiltonian)
                                print() 

                            if __name__ == "__main__":
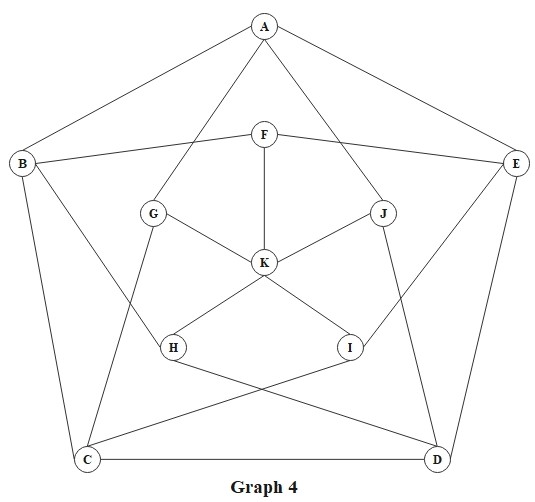
                                # Example: Graph 4
                                G_4 = [
                                [0, 1, 0, 0, 1, 0, 1, 0, 0, 1, 0],  # Vertex A
                                [1, 0, 1, 0, 0, 1, 0, 1, 0, 0, 0],  # Vertex B
                                [0, 1, 0, 1, 0, 0, 1, 0, 1, 0, 0],  # Vertex C
                                [0, 0, 1, 0, 1, 0, 0, 1, 0, 1, 0],  # Vertex D
                                [1, 0, 0, 1, 0, 1, 0, 0, 1, 0, 0],  # Vertex E
                                [0, 1, 0, 0, 1, 0, 0, 0, 0, 0, 1],  # Vertex F
                                [1, 0, 1, 0, 0, 0, 0, 0, 0, 0, 1],  # Vertex G
                                [0, 1, 0, 1, 0, 0, 0, 0, 0, 0, 1],  # Vertex H
                                [0, 0, 1, 0, 1, 0, 0, 0, 0, 0, 1],  # Vertex I
                                [1, 0, 0, 1, 0, 0, 0, 0, 0, 0, 1],  # Vertex J
                                [0, 0, 0, 0, 0, 1, 1, 1, 1, 1, 0],  # Vertex K
                                ]

                                # Use the  adjacency List 
                                adj_list_4 = matrix_to_adj_list(G_4)
                                print_adj_list(adj_list_4)
                                
                                # Valid Hamiltonian cycle
                                cycle1 = [0, 6, 2, 8, 10, 7, 1, 5, 4, 3, 9, 0]
                                print_cycle_with_result(cycle1, adj_list_4)

                                # Invalid cycle
                                cycle2 = [0, 1, 2, 3, 4, 5, 7, 6, 10, 9, 8, 0]
                                print_cycle_with_result(cycle2, adj_list_4)