Turing Machines - MATH-CS COMPASS

Turing Machines (TMs)

A Turing machine is a 7-tuple \((Q, \Sigma, \Gamma, \delta, q_0, q_{accept}, q_{reject})\) where \(Q, \Sigma, \Gamma\) are finite sets and

\(Q\) is the set of states,
\(\Sigma\) is the input alphabet not containing the blank symbol\(\, \sqcup\),
\(\Gamma\) is the tape alphabet, where \(\sqcup \in \Gamma\) and \(\Sigma \subseteq \Gamma\),
\(\delta: Q \times \Gamma \to Q \times \Gamma \times \{L, \, R\}\) is the transition function,
\(q_0 \in Q\) is the start state,
\(q_{accept} \in Q\) is the accept state, and
\(q_{reject} \in Q\) is the reject state where \(q_{accept} \neq q_{reject}\).

Here, the differences between finite automata and Turing machine:

The tape has infinite length.
A Turing machine can read symbols from the tape and write symbols on it.
The read-write head can move both to the left(L) and to the right(R).
Both reject and accept states take effect immediately.

loop

A Turing machine is more powerful than any FA and indeed, can do everything that a real computer can do. (This means that if a problem cannot be solved by a TM the problem is beyond the theoretical limits of computation.)

For each move, a Turing machine updates a configuration that is a set of three items:

Current state
Current tape contents
Current head location

For example, \[ 1001 q_5 0110 \] represents a configuration when the tape is \(10010110\), the current state is \(q_5\), and the head is currently on the third \(0\).

A Turing machine \(M\) accepts input \(w\) if there exists a sequence of configurations \(C_1, C_2, \cdots, C_k\) such that

\(C_1\) is the start configuration of \(M\) on \(w\).
\(C_i\) yields \(C_{i+1}\).
\(C_k\) is an accepting configuration.

The collection of strings that \(M\) accepts is the language of \(M\), denoted \(L(M)\). We call a language Turing-recognizable if some Turing machine can recognize it. In general, we prefer a machine does not enter the infinite loop. A language is said to be (Turing-)decidable if some Turing machine decides it, in other words, the machine always makes a decision to accept or reject.

Example: Consider a language \[ L_1 = \{0^{2^n} | n \geq 0\} \] which generates all strings of \(0\)s whose length is a power of 2.
A Turing machine \(M_1\) must decide \(L_1\):
\(M_1 = \) "On input string \(w\): "

Read left to right across the tape, crossing out every other \(0\).
If in Stage 1, the tape contained a single \(0\), accept.
If in Stage 1, the tape contained more than a single \(0\) and the number of \(0\)s was odd, reject.
Return the head to the left-hand end of the tape.
Go back to Stage 1."

\(Q = \{q_1, q_2, q_3, q_4, q_5, q_{accept}, q_{reject}\}, \, \Sigma = \{0\}, \, \Gamma = \{0, \text{ x }, \sqcup\}\), and the state diagram is as follows:

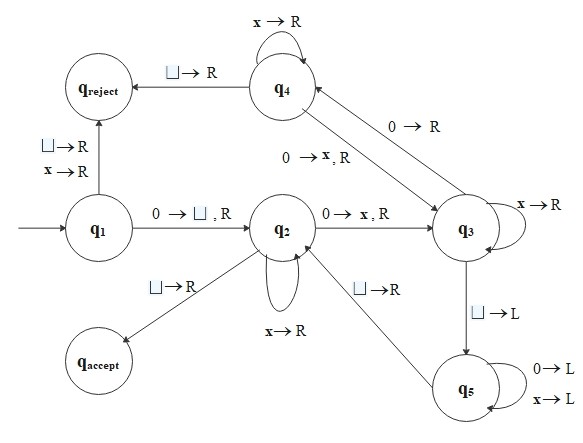
For example, if input is \(0000\), the sequence of configurations is as follows \[ \begin{align*} &q_1 0 0 0 0 \Rightarrow \sqcup q_2 0 0 0 \Rightarrow \sqcup \text{x} q_3 0 0 \Rightarrow \sqcup \text{x} 0 q_4 0 \\\\ &\Rightarrow \sqcup \text{x} 0 \text{x} q_3 \sqcup \Rightarrow \sqcup \text{x} 0 q_5 \text{x} \sqcup \Rightarrow \sqcup \text{x} q_5 0 \text{x} \sqcup \\\\ &\Rightarrow \sqcup q_5 \text{x} 0 \text{x} \sqcup \Rightarrow q_5 \sqcup \text{x} 0 \text{x} \sqcup \Rightarrow \sqcup q_2 \text{x} 0 \text{x} \sqcup \\\\ &\Rightarrow \sqcup \text{x} q_2 0 \text{x} \sqcup \Rightarrow \sqcup \text{x} \text{x} q_3 \text{x} \sqcup \Rightarrow \sqcup \text{x} \text{x} \text{x} q_3 \sqcup \\\\ &\Rightarrow \sqcup \text{x} \text{x} q_5 \text{x} \sqcup \Rightarrow \sqcup \text{x} q_5 \text{x} \text{x} \sqcup \Rightarrow \sqcup q_5 \text{x} \text{x} \text{x} \sqcup \\\\ &\Rightarrow q_5 \sqcup \text{x} \text{x} \text{x} \sqcup \Rightarrow \sqcup q_2 \text{x} \text{x} \text{x} \sqcup \Rightarrow \sqcup \text{x} q_2 \text{x} \text{x} \sqcup \\\\ &\Rightarrow \sqcup \text{x} \text{x} q_2 \text{x} \sqcup \Rightarrow \sqcup \text{x} \text{x} \text{x} q_2 \sqcup \Rightarrow \sqcup \text{x} \text{x} \text{x} \sqcup q_{accept}. \end{align*} \]

Algorithms

An algorithm can be considered as a collection of instructions for carrying out some task. Even though algorithms have had a long history in mathematics, they were not defined precisely until the 20th century. In 1936, Alonzo Church used a notational system called the \(\lambda\)-calculus to define algorithms, and Alan Turing defined algorithms with his machine, Turing machine. Moreover, theses two definitions of algorithms are equivalent(Church-Turing thesis). So, we can say that the Turing machine is a model for the definition of algorithm. In conclusion, any algorithm can be represented by a Turing machine.

We would like to learn the power and limitations of algorithms in problem-solving. It examines which problems can be solved algorithmically and which "cannot." Studying unsolvability is valuable for two main reasons. First, recognizing when a problem is algorithmically unsolvable helps in modifying or simplifying it to find a viable solution. Understanding the limitations of computers ensures they are used effectively. Second, encountering unsolvable problems provides a broader perspective on computation, sparking creativity and deeper insights into problem-solving.

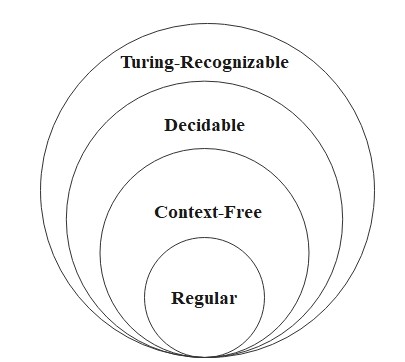
Here, we just summarize important facts about classes of languages. (Proof might be given in the future.)

Theorem:

Every context-free language(CFL) is decidable.
Some Turing-recognizable languages are undecidable.
A language is decidable if and only if it is Turing-recognizable and co-Turing-recognizable.

Note: Modern computers are essentially finite versions of Turing machines (more precisely, random-access machines (RAM) with bounded memory). Any algorithm that runs on a real computer can, in principle, be translated into a Turing machine, although it may be inefficient.

Unsolvability

Theorem: Some languages are not Turing-recognizable.

Proof: First, we show that the set of all Turing machines is countable. Note that each Turing machine \(M\) can be encoded as a finite string \(\langle M \rangle\) over some alphabet \(\Sigma\). The set of all strings \(\Sigma^*\) over the alphabet \(\Sigma\) can be written as \[ \Sigma^* = \bigcup_{n \geq 0} \Sigma^n, \] where \(n\) is any nonnegative integer, and \(\Sigma^n\) is the set of strings of length \(n\). Since each \(\Sigma^n\) is finite and a countable union of finite sets is countable, it follows that \(\Sigma^*\) is countable. Since every Turing machine \(M\) can be encoded as a finite string \(\langle M \rangle \in \Sigma^*\), the set of all Turing machines is a subset of \(\Sigma^*\). As any subset of a countable set is countable, it follows that the set of all Turing machines is countable.

Next, we show that the set of all languages is uncountable. Let \(B\) be the set of all infinite binary sequences, defined as \(B = \{b: \mathbb{N} \to \{0, 1\}\}\). It is known that \(B\) is uncountable because it can be placed in one-to-one correspondence with the power set of \(\mathbb{N}\), which has a strictly greater cardinality than \(\mathbb{N}\). Each language over \(\Sigma\) is any subset of \(\Sigma^*\). Thus, the set of all languages over alphabet \(\Sigma\) is written as \[ L = \mathcal{P}(\Sigma^*). \] Since \(\Sigma^*\) is countable, we can enumerate it as \[ \Sigma^* = \{s_1, s_2, s_3, \cdots \} \] For any language \(A \in L \), define its characteristic sequence \(\chi_A\) by \[ \chi_A (i) = \begin{cases} 1, &\text{if \(s_i \in A\)} \\ 0, &\text{if \(s_i \notin A\)} \end{cases}. \] Define the function \(f: L \to B\) by \(f(A) = \chi_A\). If \(A \neq A'\), then there exists some index \(i\) for which \(s_i\) is in one of \(A\) or \(A'\) but not the other, so \(\chi_A (i) \neq \chi_{A'} (i) \). Also, for any infinite binary sequence \(b \in B\), define the language \(A_b = \{s_i \in \Sigma^* : b(i) = 1\}\). Then \(f(A_b) = b\). Thus, \(f\) is a bijection between \(L = \mathcal{P}(\Sigma^*)\) and \(B\).
Since \(B\) is uncountable and there is a bijection \(f\) between \(L\) and \(B\), it follows that the set of all languages over \(\Sigma\) is uncountable.

Therefore, since the set of all Turing machines is countabl, and the set of all languages is uncountable, there exist languages that cannot be recognized by any Turing machine.

In conclusion, in our world there exist problems that cannot be solved by any algorithm, since some languages are not Turing-recognizable. However, while there are some problems for which no algorithm can provide an "exact" solution, the problems can be solved by effective approximation or heuristic algorithms. So, those problems are "solvable" in the practical sense.
(Many real-world problems, particularly in optimization or machine learning, are either computationally intractable or too complex to solve exactly in a reasonable amount of time. We will discuss these ideas later.)